Editor's Note:Despite the fact that chirp-OAEs were not applied widely in the clinical OAE field, they represent a considerable evolution in the TEOAE protocols. This material is mirrored from the NATASHA project web pages. The material has a technical nature and we recommend to the readers to visit Dr. Newmann's web-link for more details on this topic.
The use of chirplet stimuli are useful for evoking TEOAE in, e.g.,
clinical applications. Due to the higher level of the chirplet versus the click the
signal-to-noise ratio can be improved. Therefore the detection of an TEOAE and the
observation of saturation with increasing stimulus level is facilitated, especially when
using the ''bark'' chirplet signal. This holds especially in the case of very weak TEOAE.
In addition, the stimulation with narrowband stimuli allows a specific evaluation of the
functionality of selected basilar membrane regions in a single measurement (Neumann, 1997,
Neumann et al., 1994)
Equipment and Stimuli
a) Set-up (equipment, test environment,
etc.):
The measurement of transient evoked otoacoustic emissions TEOAE using
chirplets are almost similar to the procedures for TEOAE measurement using clicks. They
may depend on the specific setup and instrumentations. Some important aspects for the
measurement of TEOAE with chirplet signals are pointed out here:
- A sound source with a flat frequency response should be used for the acoustical
stimulation of the ear (e.g. Etymotic Research ER-2 insert ear phone). Otherwise the
chirplet stimuli may need to be adapted to compensate for the frequency response of the
sound source.
- The amplitude of four successive stimuli need to be multiplied with the factors
1,1,1,-3, respectively. This nonlinear averaging suppresses the linear response and thus
provides a better separation between stimulus and TEOAE (Bray and Kemp, 1987).
- The chirplet signals should not be longer than 3 ms to allow a separation of stimulus
and ear response.
- The acoustic response of the inner ear to the chirp stimuli should be recorded in the
sealed ear canal by using an insert ear probe (e.g. Etymotic Research ER 10 A).
- A artefact rejection and noise reduction procedure should be processed to the data, e.g.
by using a weighted averaging technique which utilizes the inverse of the respective RMS
value and/or rejecting segments with high RMS values.
- The stimulation with the chirplet signals might be carried out with the same setting of
the maximum amplitude as a click used instead. This results in an higher stimulus level of
the chirplet signal in comparison to the click stimulus due to the longer duration of the
chirplet signals.
b) Stimuli:
Fig. 1c shows a chirplet signal after applying the described correction
to the instantaneous frequency. It can be seen that the resulting chirplet signal matches
the target spectrum much better than before. In order to uniformly distribute the stimulus
energy over the entire basilar membrane, a non-uniform target spectrum can be used in the
design of the stimulus. The chirplet signal in Fig. 1d was therefore designed for a target
spectrum that is uniform on the bark scale using the formula according to ZWICKER and
TERHARDT (1980). This stimulus is in the following referred to as the ''bark'' chirplet.
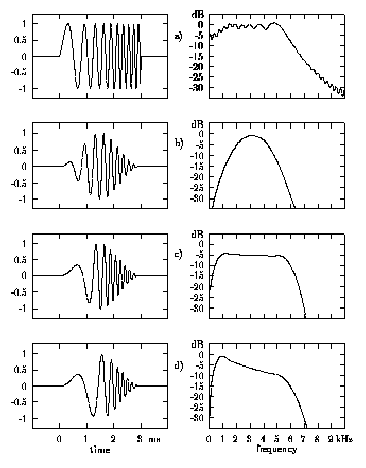 Fig. 1: Time signal and spectrum of chirplet signals with increasing instantaneous
frequency from 500 Hz to 6000 Hz: a) rectangular window, linear increase of instantaneous
frequency, b) Hanning window, linear increase of instantaneous frequency. c) Hanning
window, compensation of the window effect by a nonlinear increase of the instantaneous
frequency. d) same as c) with a target spectrum uniformly distributed on a bark scale.
Background information:
The basic idea to generate a chirplet signal for a
given power spectrum is that the spectral energy at a certain frequency increases if the
instantaneous frequency of the chirplet takes values close to this frequency during a
longer period of time. Thus, by suitably selecting the time course of the instantaneous
frequency of a signal, it is possible to manipulate its spectrum. Therefore, we specify
the chirplet signal in terms of its instantaneous frequency F(t) and its envelope A(t):
The distribution of the instantaneous frequencies can be selected to be identical to
the prescribed power spectrum L(f). Within the limitations discussed below, the
spectrum of the generated signal would match the desired spectrum. In addition, the
correspondence between the desired power spectrum and the observed power spectrum of the
signal is better if the instantaneous frequency changes slowly with time. This implies
that the instantaneous frequency function F(t) should be monotonic.
To obtain a distribution of the instantaneous frequency identical to the desired spectrum L(f),
the rate of change of the instantaneous frequency F(t) must be inversely
proportional to the spectral energy L(f) at this frequency. For example, a high
energy of a particular frequency component in the desired spectrum of the signal should
lead to a slow change of the instantaneous frequency at this particular frequency:
The envelope A(t) is not specified yet. To demonstrate the significant effect of
the envelope A(t) on the resulting signal spectrum, a rectangular and a Hanning
window is used to generate the chirplet signals shown in Figs. 1a and 1b. The signals in
these figures were calculated for a duration of 3 milliseconds with a flat target spectrum
between 500 Hz and 6000 Hz, with no power falling outside this range. Therefore, the
instantaneous frequency function increases linearly from 500 Hz to 6000 Hz. The abrupt
transitions of the signal in Fig. 1a (rectangular window) leads to an undesirable widening
of the spectrum.
This widening effect can be reduced by using a Hanning window of length T as the
envelope function A(t). The resulting signal is shown in Fig. 1b. Although the
power spectrum is now limited to the desired range, the signal still does not match the
target spectrum since the power is not uniformly distributed over the desired frequency
range. This new difficulty is caused by the weighting introduced by the Hanning window.
The reduction in signal amplitude at the beginning and at the end of the chirplet also
reduces the contributions of these regions to the power spectrum.
To compensate the power loss in the low and high frequency regions the distribution of the
instantaneous frequency is modified: Until now, the time variable used in the
instantaneous frequency function F(t) was a linear function of time. The
substitution of this time variable with a function t(t) enables a change in the
instantaneous frequency distribution. This function t(t) compensates the effect of
the weighting Hanning window by increasing with the integral of the window function. Since
a loss in signal power should be compensated, the new function t(t) is given by the
normalized integral of AČ(t):
References:
Neumann, J., S. Uppenkamp and B. Kollmeier (1994). "Chirp Evoked Otoacoustic
Emissions." Hear. Res. 79: 17-25
J. Neumann, Recording techniques, theory and audiological applications of otoacoustic
emissions (BIS Verlag, Oldenburg, 1997)
http://www.bis.uni-oldenburg.de/bisverlag/neurec97/inhalt.html
P. Bray and D. T. Kemp, "An advanced cochlear echo technique suitable for infant
screening," British Journal of Audiology 11, 191-204 (1987)
author: Kirsten Wagener
date: 1.10.1999
|



