|
| |||
Quantifying basilar membrane nonlinearity and the 'bounce' phenomenon on the nonlinearity estimated by multi-component DPOAEs
1. Introduction The active basilar membrane nonlinearity for generating multi-component DPOAEs can be modelled by a polynomial power series model at mid-lower stimulus levels (Cheng, 1999). The present study demonstrates that the degree of basilar membrane nonlinearity for generating specific multi-component DPOAEs can be quantified as 2. Measurement of multi-component DPOAEs and modelling of the basilar membrane nonlinearity At mid-lower stimulus levels the basilar membrane nonlineariry for generating multi-component DPOAEs can be modelled by a polynomial power series model (Pickles, 1988). Here only a short description of the model is given, and the details can be found elsewhere (Cheng, 1999). The multi-component DPOAEs generated by primary tones at a location on the basilar membrane, x, can be described as a polynomial power series model:
For a fixed position on the basilar membrane, the question turns to how to find the model's coefficients to match the levels of the odd order multi-component DPOAEs at lower frequencies. The even order multi-component DPOAEs were discussed (Cheng, 1999) as well. When the model's coefficients are decided, the input-output function of the basilar membrane nonlinearity to generate the specific multi-component DPOAEs can be calculated. Fig. 1 shows an example of the computer program for measuring the multi-component DPOAEs and modelling the basilar membrane nonlinearity. The left side of uppermost panel shows ear canal response while measuring the multi-component DPOAEs and the right side demonstrates the frequencies, levels and phases of different orders of DPOAEs. The middle panel demonstrates spectrum of multi-component DPOAEs. The lowest panel shows the input-output function of the basilar membrane nonlinearity, the polynomial power series model and quantifying basilar membrane nonlinearity. 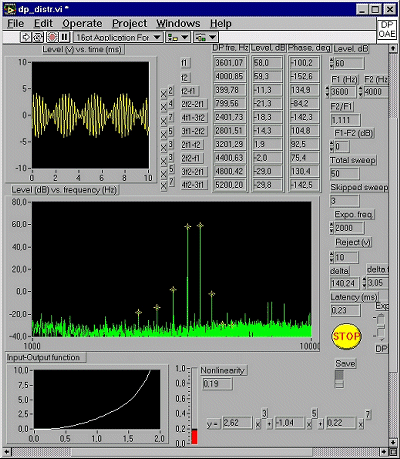 Fig.1 3. Quantifying basilar membrane nonlinearity The input-output function can be calculated from the multi-component DPOAEs at mid-lower stimulus levels by applying a polynomial power series model. For a nonlinear system, as a result of the system nonlinearity, the error energy between model's output y(n) and model's input x(n) of the system can be estimated as:
where a is a scale factor. Let
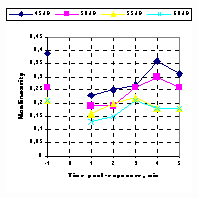
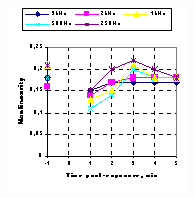
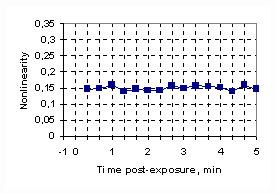
where 4. Experimental protocol a Fig. 2. (a) Two examples of the 'bounce' phenomenon after the normal-hearing ears are exposed to a low-frequency tone for 1 minute. The nonlinearity at -1 minute post-exposure time indicated the basilar membrane nonlinearity before the low-frequency tone exposure and the nonlinearity from 20 second to 5.0 minutes indicated the basilar membrane nonlinearity after the low-frequency tone exposure. (b) Reliability of the measurement of the basilar membrane nonlinearity for the ear of the lower curve in Fig. 2a. The measurement was done for the post-exposure time without the low-frequency tone exposure. 5. 'Bounce' effect on basilar membrane nonlinearity as a function of stimulus parameters
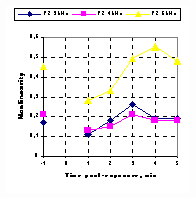
Fig. 3. 'Bounce' phenomenon on the basilar membrane nonlinearity as a function of stimulus parameters: a (left panel)as a function of stimulus levels; b (middle panel)as a function of exposure tone frequencies; and c (right panel) as a function of F2 frequency. 6. References Cheng, J. (1999). "Estimation of active cochlear nonlinearity by multi-component distortion-product otoacoustic emissions," Acustica 85, 721-727. Hirsh, I. J., and Ward, P. H. (1952). "Recovery of the auditory threshold after strong acoustic stimulation," J. Acoust. Soc. Am. 24, 131-141. Kemp, D. T. (1986). "Otoacoustic emissions, travelling waves and cochlear mechanism," Hearing Res. 22, 95-104. Kirk, D. L., Moleirinho, A., and Patuzzi, R. B. (1997). "Microphonic and DPOAE measurements suggest a micromechanical mechanism for the 'bounce' phenomenon following low-frequency tones," Hearing Res. 112, 69-86. Kirk, D. L., and Patuzzi, R. B. (1997). "Transient changes in cochlear potentials and DPOAEs after low-frequency tones: the 'two minute bounce' revisited," Hearing Res. 112, 49-68. Pickles, J. O. (1988). An introduction to the physiology of hearing (Academic Press, London, 2nd ed.), pp. 106-109. |
 |  |


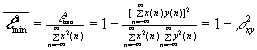 , (3)
, (3)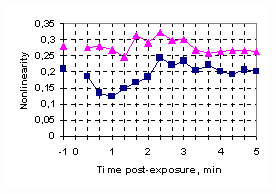
 b
b