A New Signal Processing Technique for the Estimation of DPOAE Signals

Alireza K. Ziarani

Department of Electrical and Computer Engineering, Clarkson University, Potsdam, NY, USA 13699-5720

E-mail: Alireza K. Ziarani

Telephone: (315) 268-4278

Fax: (315) 268-7600

 

 

 

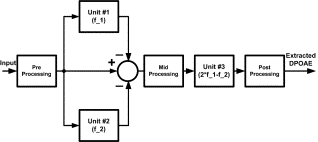
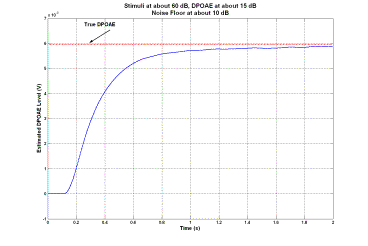
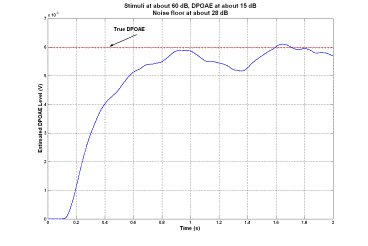
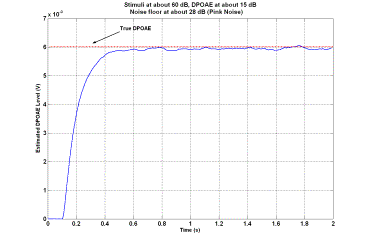
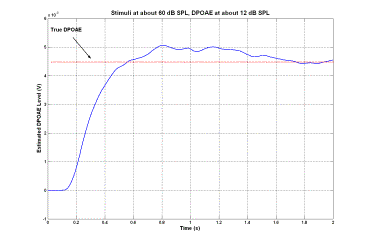
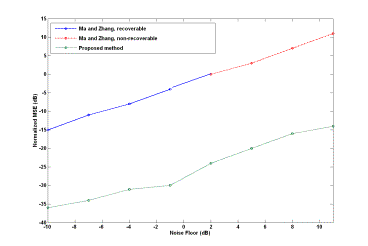
1.    Introduction

Distortion product otoacoustic emissions (DPOAEs) are very low level stimulated acoustic responses to two pure tones presented to the ear canal. DPOAE measurement provides an objective non-invasive measure of peripheral auditory function and is used for hearing assessment especially in newborns [1]. DPOAEs have been recognized for a number years [2, 3]. However, DPOAE measurement is considered an active area of research because of the challenging nature of the signal processing task.

In this type of otoacoustic test, two pure tones with frequencies f₁ and f₂ are presented to the cochlea. For best results, f₂ is usually chosen as 1.2f₁. Since the ear is a nonlinear structure, a number of very low level distortion products are generated due to the inter-modulation process within the cochlea. Among various distortion products, the component with frequency f_d=2f₁-f₂ is usually the strongest. The level of such a distortion product (commonly referred to as the DPOAE signal) is taken as an index of the functionality of the ear. Estimation of such a weak signal buried under two strong stimuli and other inter-modulations in a potentially noisy background is a challenging signal processing problem.

Conventionally, the discrete Fourier transform (DFT) has been used as the main signal processing tool to estimate the level of the DPOAE signals. Application of the DFT to this problem has a number of shortcomings, among which the long measurement time is the most pronounced one [4]. Long measurement time is usually required for the acquisition of a sufficiently large amount of data which, when averaged, will reduce the overall background noise effect. In addition to the need to increase the measurement time, the tests are usually required to be conducted in low noise environments such as sound-proof rooms or other types of sound-proof enclosures.

In an attempt to devise high performance DPOAE estimation techniques, adaptive signal processing techniques and maximum-likelihood estimators have been employed. Such techniques generally offer better performance in terms of measurement time which may be interpreted as their higher noise immunity compared to that of the DFT.

This paper presents an overview of a recently developed method of DPOAE signal measurement, which employs, as its main building block, a recently introduced nonlinear adaptive signal processing algorithm [5]. The formulation, mathematical properties and DSP implementation of the employed signal processing algorithm are presented in [6] where detailed discussions on the stability and convergence issues of the algorithm are also presented. Some of the applications of the employed algorithm in diverse areas of engineering are presented in [7, 8].

2.    Method

The proposed signal processing method employs three units of the algorithm presented in [6] to construct a high performance DPOAE estimation algorithm. Each unit is capable of focusing on and extracting a pre-specified sinusoidal component of its input signal which may contain other components and noise. More importantly, it can effectively follow variations in the amplitude, phase (and frequency) of the extracted sinusoidal component. Although the underlying mathematics ensuring the stability and performance of such an algorithm is very complex, its structure remains extremely simple. It is found to be very robust with respect to variations in the internal settings of the controlling parameters, as well as external conditions such as the presence of noise, and exhibits superior performance over existing linear adaptive and DFT-based algorithms in terms of convergence speed versus accuracy trade-off.

The input DPOAE signal is often assumed to consist of two pure sinusoids with frequencies f₁ and f₂ at a very high level (usually about 50 to 70 dB SPL) and a very low level DPOAE 2f₁-f₂ at about -5 to 15 dB SPL. It is contaminated by a noise usually considered to be about 0 to 20 dB SPL. In fact, the noise represents the totality of all undesired signals that may be present in the environment in which the examination is being conducted, the sum of all generated inter-modulations as well as the unavoidable background noise. It has been observed that the estimation error increases with the increase of the amount of background noise. This can be compensated by re-adjusting the parameters of the algorithm to reduce the error at the expense of the convergence speed. Because of the excessive degree of the noise, one single unit assigned to extract the DPOAE signal out of the input signal exhibits poor performance in terms of the estimation error, (or the convergence speed).

Figure 1 . Block diagram representation of the proposed method of DPOAE estimation.

In the block diagram of Figure 1, the first two units are assigned to extract the two stimuli. They effectively do so with very small errors. The extracted stimuli are then subtracted from the input signal to produce a signal, of which DPOAE has a higher relative portion. The third unit is then set to extract the DPOAE signal. To further enhance the performance of the DPOAE estimator, some pre-processing, post-processing as well as intermediary filtering stages have been added. The stage of pre-processing consists of preliminary normalization and band-pass filtering. The purpose of the normalization process is to amplify the input signal to bring it to a certain level on the basis of which the setting of the parameters of the units may be adjusted. The band-pass filtering is intended to attenuate all components except the DPOAE signal as much as possible to enhance the quality of the input signal. This can be achieved by means of a simple second order band-pass filter, the center frequency of which is set to be that of the DPOAE signal.

The intermediate signal out of which the two stimuli are removed may be directly input to a third unit for the extraction of the DPOAE signal. Since elimination of the two stimuli needs certain convergence time, at the very early initial moments a large portion of the two stimuli exists which will set the initial operational point of the third unit too far away from the true level of the DPOAE signal. To overcome this, a time-gating process may be employed to delay the transfer of the intermediate signal to the third unit. This is accommodated in the mid-processing unit of Figure 1. The output of this unit is zero and remains zero for a short period of time until a more or less steady state condition for the two units is achieved. The mid-processing may also include some normalization and band-pass filtering just like the pre-processing stage. The post-processing unit consists of de-normalization of the DPOAE signal and its level to restore the original values as well as some (low-pass) filtering to further smooth out the estimate of the DPOAE signal and its level.

3.    Results

Performance of the proposed method is demonstrated in this section using both flexibly controlled simulated data and a set of real clinically recorded signal.

3.1 Simulated Data

For the simulations presented in this section, the frequency of the first stimulus f₁ varies over the range of 500 to 4000 Hz. For each numerical experiment, f₁ is randomly generated within this range. The frequencies of the second stimulus and the DPOAE are then set as f₂=1.2f₁ and f_d=2f₁-f₂, respectively. The initial phases of the simulated stimuli and the DPOAE are randomly chosen within 0 to 180 degrees. The simulated noise added to the input signal is a zero-mean white Gaussian noise for the first two experiments and is a pink Gaussian noise for the third experiment. The levels of the stimuli, DPOAE and noise floor are specified in each case.

Figure 2 presents the performance of the proposed DPOAE estimator when the levels of the two stimuli are randomly generated within the range of 0.8 to 1 V (roughly corresponding to a relative 60 dB level) while the DPOAE signal has a level of about 6 mV (corresponding to a relative 15 dB level). The noise floor is at about 10 dB. The conditions in this example are in accordance with the defined conditions of the problem. It is observed that the convergence is achieved well within the desired one second test period with a small estimation error. In another numerical experiment, the level of the noise floor is increased about four times (corresponding to about 28 dB level). Figure 3 shows the estimation process. The estimation is achieved well within the desired one second test period with a tolerable estimation error. The present parameter setting easily accommodates noise levels of up to 30 dB, which is believed to be an exaggeration of the actual scenarios. However, if the expected noise floor happens to be even higher, one can sacrifice the speed by re-adjusting the parameter settings. Generally, one needs to take into account the following factors when choosing the values of parameter settings: some idea about the potential background noise, the desired speed of convergence and the tolerable error. Experience of the authors as well as that of the collaborators in companies manufacturing DPOAE measurement equipment confirms the suitability of the suggested parameter settings in practical DPOAE measurement tests.

Figure 2 . Illustration of the performance of the proposed DPOAE estimator using simulated data.

Figure 3 . Illustration of the performance of the proposed DPOAE estimator using simulated data. Compared to the conditions of Figure 2, the noise floor in increased about four times.

Typical environmental noise experienced during the recording of signals within the acoustic range is pink, in which the power density decreases with increasing frequency over a finite frequency range so that each octave contains the same amount of power. To present a more realistic demonstration of the performance of the proposed method, the experiment of Figure 3 is repeated using a pink background noise. Figure 4 illustrates the estimation process where f₁ is about 3500 Hz. It is observed that the performance of the proposed method is better in this case as opposed to the case of the contamination by white noise (Figure 3). This can be explained by the fact that given the non-uniform distribution of the noise power, less noise exists around the frequencies of interest. This renders the estimation process more accurate. Further experiments show that at lower frequencies, the effect of pink noise is more destructive than that of the white noise, as would be expected theoretically.

Figure 4 . Illustration of the performance of the proposed DPOAE estimator using simulated data. This is the same experiment as that of Figure 3, but with pink background noise.

Figure 5 . Illustration of the performance of the proposed DPOAE estimator using a set of clinically recorded data.

3.2 Recorded Data

One set of clinical data recorded at Rotman Research Institute of the University of Toronto is used to verify the functionality of the proposed method. The recording is conducted using specialized otoacoustic probes. About 20 seconds of recording is available. The total length of the recording is used to obtain the frequency spectrum of the signal, which in turn can serve as a means of guessing the true value of the DPOAE level. The frequencies of the two stimuli and the DPOAE are f₁=1618, f₂=1797 and f_d=1438 Hz, respectively. Figure 5 presents the performance of the proposed method. It is observed that the convergence is achieved within the desired one second test period with a small estimation error.

Figure 6 . Comparison of the performance of the proposed method with the method of Ma and Zhang [9].

4.    Discussion

One of the recently proposed methods presented by Ma and Zhang in [9] is used in this section for a quantitative comparison with the proposed method. The method presented in [9] is an optimal maximum-likelihood estimator for the extraction of DPOAE signals. Superior performance of the method, especially in cases where DFT exhibits leakage effect is observed. The signal model is assumed to consist of the two stimuli and the DPOAE signal with noise. In [9], simulated data are used for the two stimuli and the DPOAE signal whereas the background noise is a recorded noise.  

Simulated data were used for the comparison of the method of Ma and Zhang with the proposed method. Similar results to those presented in [9] were obtained using a simulated noise of zero-mean white Gaussian distribution as the background noise. For both cases, the numerical experiments involve two stimuli of frequencies f₁=2.454 kHz and f₂=3.003 kHz. The DPOAE signal is thus at f_d=2f₁-f₂=1.905 kHz. The sampling frequency is chosen as f_s=10.24 kHz. The DPOAE signal is at 0 dB level while the two stimuli are at 65 dB. The experiment was repeated several times for different levels of the noise floor. Figure 6 compares the performance of the two methods for varying levels of the noise floor. The index of the performance is taken to be the normalized mean squares error (MSE) incurred in the estimation process. In the case of the proposed method, the vector of the estimated level of the DPOAE is formed after the signal is stabilized in the time domain (after about 500 ms delay).

When the incurred error exceeds the signal level, the signal is no longer recoverable. It is observed that the proposed method is less sensitive to the level of the background noise. In fact, as soon as the noise level exceeds the DPOAE level, the signal is totally lost and the estimation process fails. The proposed method of this paper has a very high degree of noise immunity, about 20 dB more than that of Ma and Zhang.

5.    Conclusions

A method of measurement of DPOAE signal level employing a recently introduced nonlinear adaptive signal processing technique is presented. Performance of the proposed method is demonstrated using both simulated and real clinical data, and a comparison of its performance with that of one of the existing methods is presented. The main features of the proposed method of DPOAE signal measurement are its 1) structural simplicity, 2) high noise immunity and robustness, and 3) relatively high speed of convergence. Given the low complexity of the proposed method, it requires low level of computational resources, which in turn translates into less expensive equipment. High noise immunity and robustness of the proposed method render it suitable for practical clinical examinations which may be conducted in highly noisy backgrounds, perhaps without involving sound-proof examination rooms. This again translates into less expensive medical equipment. Also, given that the reduction in the level of the stimuli translates into a higher relative degree of background noise, the high noise immunity feature of the proposed method may be used to reduce the level of the stimuli for a more patient friendly examination. High speed of convergence of the proposed method is useful in reducing the examination time which again results in a more patient friendly and time effective clinical examination.

6.    References

[1] R. E. Delgado, Ö. Özdamar, S. Rahman and C. N. Lopez,, “Adaptive noise cancellation in a multimicrophone system for distortion product otoacoustic emission acquisition,” IEEE Transactions on Biomedical Engineering, vol. 47, no. 9, pp. 1154-1164, 2000.

[2] D. T. Kemp, “Stimulated acoustic emissions from within the human auditory system,” Journal of Acoustical Society of America, vol. 64, no. 5, pp. 1386-1391, 1978.

[3] R. Probst, B. L. Lonsbury-Martin and G. K. Martin, “A review of otoacoustic emissions,” Journal of Acoustical Society of America, vol. 89, no. 5, pp. 2027-2067, 1991.

[4] X. Li, Y. Sokolov and H. Kunov, “System and method for processing low signal-to-noise ratio signals,” PCT Patent Application, filed on November 8th, 1999, international publication date: May 18th, 2000, international application number: PCT/CA99/01055.

[5] A. K. Ziarani and A. Konrad, “A novel method of estimation of DPOAE signals,” IEEE Transactions on Biomedical Engineering, vol. 51, no. 5, pp. 864-868, 2004.

[6] A. K. Ziarani and A. Konrad, “A method of extraction of nonstationary sinusoids,” Signal Processing, vol. 84, no. 8, pp. 1323-1346, 2004.

[7] A. K. Ziarani and A. Konrad, “A nonlinear adaptive method of elimination of power line interference in ECG signals,” IEEE Transactions on Biomedical Engineering, vol. 49, no. 6, pp. 540-547, 2002.

[8] A. K. Ziarani, A. Konrad and A.N. Sinclair, “A novel time-domain method of analysis of pulsed sine wave signals,” IEEE Transactions on Instrumentation and Measurement, vol. 52, no. 3, pp. 809-814, 2003.

[9] W. K. Ma and Y. T. Zhang, “Estimation of distortion product otoacoustic emissions,” IEEE Transactions on Biomedical Engineering, vol. 46, no. 10, pp. 1261-1264, 1999.